Степень числа: что это такое в математике и как правильно возводить в степень

Арифметика начинается с простых действий. Затем более сложные вычисления открывают путь в мир математики. Среди них возведение числа в степень, для которого существуют строгие правила.

Зачем и по каким правилам возводят числа в степень

Что такое степень числа? При решении задач иногда приходится одно число умножить само на себя много раз. Такое действие называется возведением числа в степень.

Например, запись умножения числа на себя будет выглядеть так: a×a×a×a×a. И так нужное количество раз (n). Принято сокращать такие выражения, тогда запись в общем виде выглядит так: aⁿ. В этой формуле:

а — основание степени, то есть число, которое надо возвести в степень, а именно умножить на себя несколько раз;
n — показатель степени или количество операций умножения.

Принято несколько вариантов прочтения таких выражений:

a в степени n;
n-ая степень числа а;
а в n-ой степени.

Есть общепринятые особые случаи прочтения чисел в степени. Например:

а² (число во 2-й степени) читается как «а в квадрате»;
а³ (число в 3-й степени) читается как «а в кубе».

Как найти степень числа? Степень — это многократное умножение числа на себя. Чтобы найти степень числа, надо умножить его само на себя столько раз, сколько указано в показателе степени.

При решении примеров и задач возведением в степень называется нахождение числового значения числа после его возведения в степень. Например, надо вычислить выражение 2 в 4 степени. Это значит, число 2 умножается на себя 4 раза (2×2×2×2=16). Сокращенно записывается так: 2⁴=16.

Платформа самостоятельного обучения GCF Global подтверждает, насколько удобны записи возведения в степень: они сокращают и упрощают сложные примеры или представляют выражения в более компактной форме.

Следует запомнить особые случаи, которые встречаются при выполнении возведения в степень:

число в степени 1 — само это число (а¹=а);
число в степени 0 равно 1 (а⁰=1);
0 при возведении в любую степень равен 0 (0ⁿ=0);
1 в любой степени равна 1 (1ⁿ=1);
0 в степени 0 в математике считается лишенным смысла.

Удобно при решении задач пользоваться таблицей степеней:

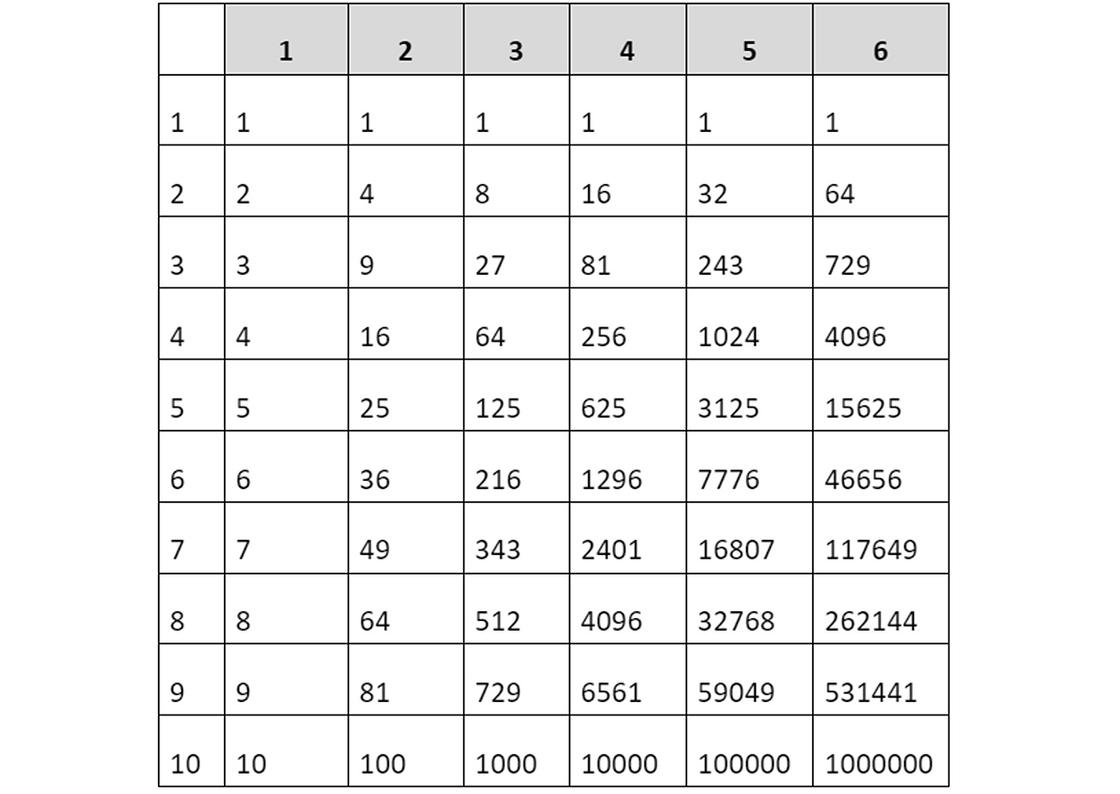
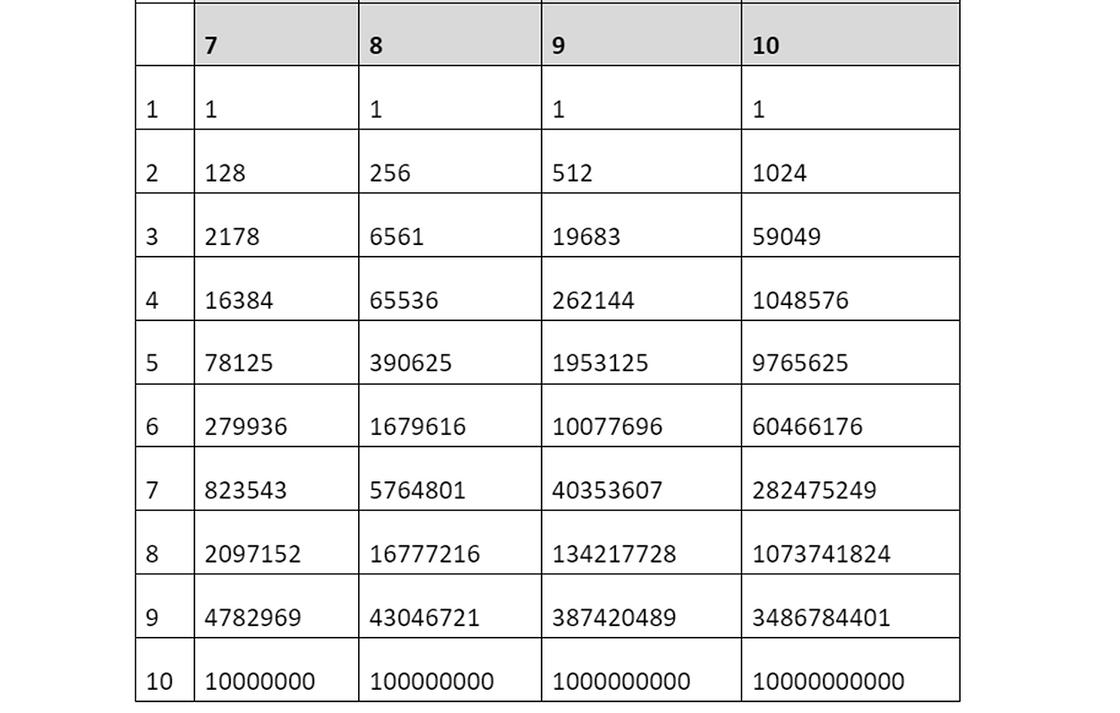
В этой таблице в первом столбце находятся числа, которые надо возвести в степень (основания). В первой строке — показатели степени. Надо определить оба необходимых показателя и на пересечении столбца и строки найти результат.

В математике существуют несложные правила по возведению чисел в степень, которые подсказывает математический онлайн-сервис Math Planet:

При умножении чисел с одинаковым основанием и разными степенями степени складываются: а²×а³=а⁵.
При делении чисел с одинаковым основанием степени вычитаются: а⁴÷а²=а². Если показатель степени 1-го числа меньше показателя степени 2-го, тогда число возводится в отрицательную степень.
При возведении числа в отрицательную степень результат будет обратный числу с положительной степенью: а⁻²=1/а².
При возведении степени в степень показатели степеней перемножаются: (а²)³=а⁶.

Эти несложные правила следует запомнить и придерживаться при решении примеров. Важно при этом также хорошо знать таблицу умножения.

Разные варианты и порядок возведения чисел в степень

Возведение положительных чисел в степень выполняют по рассмотренным правилам. Сложности могут возникнуть, если надо возвести в степень отрицательное число. В результате может получиться как положительное, так и отрицательное число. Почему так происходит? Ответ находим в правилах умножения отрицательных чисел, то есть чисел со знаком минус:

При перемножении двух отрицательных чисел получаем положительное число (минус×минус=плюс): (–2)×(–2)=4.
При умножении отрицательного числа на положительное получается отрицательное число (минус×плюс=минус): (–2)×2= –4.

При возведении отрицательного числа в степень будет иметь решающее значение, в какую степень его надо возвести — в чётную или нечетную:

При возведении в чётную степень число будет умножено само на себя чётное число раз, в результате получится положительное число: (–3)²=(–3)×(–3)=9.
При возведении в нечетную степень основание будет умножено на себя нечетное число раз. Например, надо возвести в 3 степень число –2, то есть (–2)×(–2)×(–2). При умножении первых двух отрицательных чисел получим положительное число, при умножении его на следующее отрицательное число получим отрицательное. Таким образом, в результате всего вычисления получится отрицательное число: (–2)³= (–2)×(–2)×(–2)=4×(–2)= –8.

Пример возведения отрицательного числа в степень

Часто при возведении в степень отрицательного числа допускают ошибки. Следует знать, что похожие выражения с отрицательными основаниями, которые встречаются в примерах, всё-таки различны и вычисляются по разным правилам. Например, рассмотрим выражение (–5)⁴ и похожее на него –5⁴:

Выражение (–5)⁴ означает, что надо найти значение 4-й степени отрицательного числа 5. Вычисляется оно так: (–5)⁴= (–5)×(–5)×(–5) ×(–5)=625.
Выражение в примере –5⁴ означает, что надо вычесть число 5 в 4-й степени. В этом случае число 5 сначала возводят в степень: 5⁴=625. Затем перед полученным результатом ставят минус, что означает в примере, что его надо вычесть, то есть выполнить действие вычитания.

При решении сложных примеров со степенями существует правило, которое регулирует порядок выполнения действий. Правилом установлено:

Первым действием выполняется возведение в степень.
Во вторую очередь производится умножение или деление.
После всего выполняется сложение и вычитание.

Если в примере есть скобки, то в таком же порядке выполняются действия в скобках, потом оставшиеся действия в той же последовательности. Например: при решении примера [(–2)⁴+(–1) ³×7]÷(–3)² следует делать вычисления в таком порядке: